Bài giảng Đại số Lớp 7 - Tiết 47: Số trung bình cộng

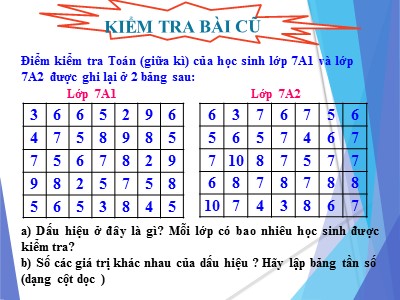
KIỂM TRA BÀI CŨĐiểm kiểm tra Toán (giữa kì) của học sinh lớp 7A1 và lớp 7A2 được ghi lại ở 2 bảng sau:3665296475898575678299825758565384563767 56565746771087577687878810743867Lớp 7A1Lớp 7A2a) Dấu hiệu ở đây là gì? Mỗi lớp có bao nhiêu học sinh được kiểm tra?b) Số các giá trị khác nhau của dấu hiệu ? Hãy lập bảng tần số (dạng cột dọc ) ĐÁP ÁNb) Số các giá trị khác nhau của dấu hiệu : - Lớp 7A1: là 8- Lớp 7A2 : là 7Lớp 7A1Lớp 7A2Điểm số(x)Tần số(n)2345678932295464Điếm số(x)Tần số(n)34567810 2 2 4 712 6 2a) Dấu hiệu: Điểm kiểm tra toán (giữa kì) của mỗi học sinh lớp 7A1 và 7A2. Mỗi lớp có 35 học sinh được kiểm traLập bảng tần số (dạng cột dọc )N= 35 N= 35 Hai lớp 7A1 và 7A2 cùng một giáo viên dạy môn Toán và cùng làm một bài kiểm tra 1 tiết. Sau khi có kết quả, muốn biết lớp nào làm bài tốt hơn thì ta phải làm như thế nào?TIẾT 47:SỐ TRUNG BÌNH CỘNG?1. Hãy tính trung bình cộng của dãy số sau: 5; 3; 8; 6Trung bình cộng là: ( 5 + 3 + 8 + 6 ) : 4 = 5,5?2. Tính trung bình cộng của dãy số sau: 2; 2; 2; 6; 9; 7; 7Trung bình cộng là: ( 2 + 2 + 2 + 6 + 9 + 7 + 7 ) : 7 = 5,0Cách khác:TIẾT 47: SỐ TRUNG BÌNH CỘNG1. Số trung bình cộng của dấu hiệu ( ký hiệu ) Phân tích: giá trị 2 có tần số là 3, giá trị 6 có tần số là 1, giá trị 9 có tần số là 1, giá trị 7 có tần số là 2 và số các giá trị N = 7. Lúc này để tính trung bình cộng ta cần: Nhân từng giá trị với tần số tương ứng Cộng tất cả các tích vừa tìm được Chia tổng đó cho số các giá trị ( tức tổng các tần số)Dựa vào phân tích trên ta có bảng sau:Điểm số (x)Tần số (n)2332425965748694 N= 35Các tích (x.n) 20735=≈ 5,9 6 6 84530284836Tổng:(x1 ) (x2 ) (x3 ) (xk ) ....207(n1)(n2)(n3)(nk)....Lớp 7A1(x1n1) (x2n2) (x3n3) (xknk) ....1. Số trung bình cộng của dấu hiệu ( ký hiệu ) TIẾT 47: SỐ TRUNG BÌNH CỘNGCách tính số trung bình cộng: Nhân từng giá trị với tần số tương ứng Cộng tất cả các tích vừa tìm được Chia tổng đó cho số các giá trị ( tức tổng các tần số)Công thức tính:1. Số trung bình cộng của dấu hiệu ( ký hiệu ) Trong đó:x1, x2, x3 xk là các giá trị khác nhau của dấu hiệu Xn1, n2, x3 nk là các tần số tương ứngN là số các giá trịTIẾT 47: SỐ TRUNG BÌNH CỘNGĐiểm số (x)Tần số (n)3 24 25 46 77128 610 2N= 35Các tích (x.n)Lớp 7A26 82042844820Tổng:22822835=≈ 6,520735=≈ 5,9Lớp 7A1:Hãy so sánh kết quả học tập môn toán của 2 lớp ?Dựa vào điểm trung bình cộng môn Toán của hai lớp thì khả năng học môn Toán lớp 7A2 học tốt hơn lớp 7A1Qua bài toán trên ta đã dùng số trung bình cộng để: Đánh giá kết quả học tập môn toán của một lớp ( tức là làm “đại diện” cho dấu hiệu) So sánh khả năng học môn toán của hai lớp ( So sánh 2 dấu hiệu cùng loại )2. Ý nghĩa của số trung bình cộng Số trung bình cộng thường được dùng làm “ đại diện” cho dấu hiệu, đặc biệt là khi muốn so sánh các dấu hiệu cùng loại▼Chú ý : Khi các giá trị của dấu hiệu có khoảng chênh lệch rất lớn đối với nhau thì không nên lấy số trung bình cộng làm“đại diện” cho dấu hiệu đóVí dụ: Xét dấu hiệu X có dãy giá trị là : 4000; 1000; 500; 100Không thể lấy số trung bình cộng làm đại diện cho X vì có sự chênh lệch rất lớn giữa các giá trị (chẳng hạn, 4000 và 100) Số trung bình cộng có thể không thuộc dãy giá trị của dấu hiệuVí dụ: Một cửa hàng bán dép ghi lại số dép đã bán cho nam giới trong một quý theo các cỡ khác nhau ở bảng sau:Cỡ dép (x)363738404142Số dép bán được (n)1345110126405N=52339184Xét ví dụ : Sau một tháng bán hàng người bán hàng sẽ kiểm kê lại các mặt hàng đã bán .Vậy khi đó người bán hàng sẽ chú ý đến điều gì ? Giá trị 39 với tần số lớn nhất (184) được gọi là mốt.1. Số trung bình cộng của dấu hiệu Công thức:2. Ý nghĩa của số trung bình cộng ▼Chú ý : sgk/19Ý nghĩa: Số trung bình cộng thường được dùng làm “ đại diện” cho dấu hiệu, đặc biệt là khi muốn so sánh các dấu hiệu cùng loại3. Mốt của dấu hiệu Mốt của dấu hiệu là giá trị có tần số lớn nhất trong bảng “tần số”; kí hiệu là M0TIẾT 47: SỐ TRUNG BÌNH CỘNGCỦNG CỐĐiểm (x)Tần số (n)Tích (x.n)678244N =10Tổng:HỌC SINH AĐiểm (x)Tần số (n)Tích (x.n)56891023221N =10Tổng:HỌC SINH B72122832101018161872Điền vào bảng các giá trị của tích (x.n)Tính số trung bình cộngBài 1: Điểm kiểm tra học kì của hai học sinh trong lớp được ghi lại hai bảng sau:CỦNG CỐBài 2 (14 – SGK/20): Hãy tính số trung bình cộng của dấu hiệu ở bài tập 9 3107810964878109588668887610587884105479Thời gian giải một bài toán (tính theo phút) của 35 h/s được ghi trong bảng 14Bảng 143107810964878109588668887610587884105479Thời gian (x)Tần số (n)Các tích (x.n)314353647581193105N=35312152435882750Tổng: 254Bài 3: (15 – SGK/20)a) Dấu hiệu cần tìm hiểu ở đây là gì và số các giá trị là bao nhiêu?b) Tính số trung bình cộngc) Tìm mốt của dấu hiệua) Dấu hiệu: Tuổi thọ của mỗi bóng đèn. Có 50 giá trịb) Tính số trung bình cộngTuổi thọ (x)Số bóng đèn tương ứng (n)Các tích (x.n)115051160811701211801811907N = 505750928014040212408330Tổng: 58640Lời giảic) Mốt của dấu hiệu là:1. Công thức tính số trung bình cộng2. Ý nghĩa của số trung bình cộngSố trung bình cộng thường được dùng làm “đại diện” cho dấu hiệu, đặc biệt là khi muốn so sánh các dấu hiệu cùng loại.3. Mốt của dấu hiệuMốt của dấu hiệu là giá trị có tần số lớn nhất trong bảng “tần số”; kí hiệu là M0 . GHI NHỚLàm bài tập 17 , 18 (tr 20, 21 - SGK).Chúc các em học tập tốt