Bài giảng Toán Lớp 7 - Bài 4: Tính chất ba đường trung tuyến của tam giác

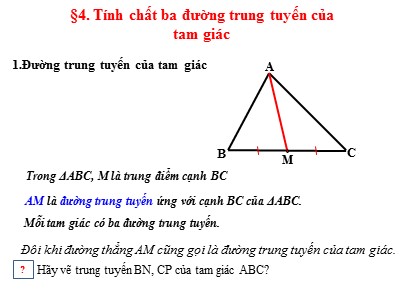
1.Đường trung tuyến của tam giácMỗi tam giác có ba đường trung tuyến.MCBAAM là đường trung tuyến ứng với cạnh BC của ΔABC.Trong ΔABC, M là trung điểm cạnh BC Đôi khi đường thẳng AM cũng gọi là đường trung tuyến của tam giác.Hãy vẽ trung tuyến BN, CP của tam giác ABC??§4. Tính chất ba đường trung tuyến của tam giácBài tập 1: Cho AM là đường trung tuyến trong tam giác ABC. Hình vẽ nào sau đây là đúng?ABCHHình 1ABCDHình 2aABCMHình 3ABCIHình 4Bài tập 2: Chọn phát biểu đúng về định nghĩa đường trung tuyến trong tam giác?Đường trung tuyến trong tam giác là đường thẳng đi qua một đỉnh của tam giác.B. Đường trung tuyến trong tam giác là đường thẳng đi qua trung điểm một cạnh của tam giác.C. Đường trung tuyến trong tam giác là đường thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện.D. Đáp án khác.Định lí:Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng độ dài đường trung tuyến đi qua đỉnh ấy.ABCEFGDTam giác ABC có AD, BE, CF là ba trung tuyến đồng quy tại G, ta có:Điểm G gọi là trọng tâm của tam giác ABC§4. Tính chất ba đường trung tuyến của tam giác2. Tính chất của 3 đường trung tuyếnGBCEFACách 1: Tìm giao điểm của hai đường trung tuyếnCách xác định trọng tâm G của tam giác ABC GBCDACách 2:Vẽ một đường trung tuyến, vẽ G cách đỉnh bằng 2/3 độ dài đường trung tuyến đóHãy điền từ hoặc cụm từ thích hợp vào chỗ trống trong các câu sau:3. Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng .. độ dài đường trung tuyến cùng đi qua một điểm2. Ba đường trung tuyến của tam giác ....... điểm đó được gọi là trọng tâm của tam giácBài tập 3:Đường trung tuyến của tam giác là đoạn thẳng nối từ của tam giác tới đi qua đỉnh ấy.đỉnhtrung điểm cạnh đối diện.Bài 23 (SGK trang 23)DEHGFCho G là trọng tâm của tam giác DEF với đường trung tuyến DH. Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai ?ĐĐSĐBài 24 (SGK trang 66) Cho hình vẽ, điền số thích hợp vào chỗ trống: MG = .MR; GR = .MR; GR = MG NS = NG; NS = GS; 	 NG = GS NRPSGMBài 26 SGK trang 67 Chứng minh định lí: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.Vì ΔABC cân tại A nên AB=ACVì M,N lần lượt là trung điểm của 2 cạnh AC và AB, suy ra:AN = BN = AM = CM = Xét ΔBCM và ΔCBN có:+) Cạnh BC chung+) = (do ΔABC cân)+) CM = BN (chứng minh trên)Vậy ΔBCM = ΔCBN (c.g.c)⇒ BM = CN (điều phải chứng minh).GIẢIBài 28 SGK trang 67 Cho tam giác DEF cân tại D với đường trung tuyến DI.Chứng minh ΔDEI = ΔDFI. Cho biết số đo của hai góc DIE và DIF.Biết DE = DF = 13cm, EF = 10cm, hãy tính độ dài đường trung tuyến DI.a) Xét ΔDEI và ΔDFI có:+) DI là cạnh chung+) DE=DF (vì ΔDEF cân tại D)+) IE=IF (DI là trung tuyến)Vậy ΔDEI=ΔDFI (c.c.c)b) Vì ΔDEI=ΔDFI (theo câu a) nên Mà ( hai góc kề bù)⇒ Vậy các góc DIE và góc DIF là những góc vuông.c) I là trung điểm của EF nên Áp dụng định lí Pytago vào ΔDEI vuông tại I (do theo câu b góc DIE vuông) ta có:⇒DI = 12DEFIGIẢIHƯỚNG DẪN TỰ HỌCHọc thuộc tính chất của ba đường trung tuyếnLàm bài 25, 27, 29, 30 SGK trang 67Làm bài tập trên google form lấy điểm 15 phút.