Bài giảng Hình học Khối 7 - Bài 3: Quan hệ giữa ba cạnh của một tam giác - Bất đẳng thức tam giác

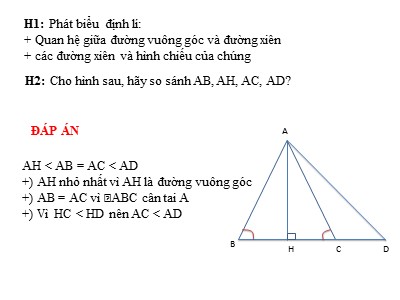
H1: Phát biểu định lí:+ Quan hệ giữa đường vuông góc và đường xiên+ các đường xiên và hình chiếu của chúngH2: Cho hình sau, hãy so sánh AB, AH, AC, AD?AHBCDĐÁP ÁNAH BE ED 5; 3 + 5 > 4; 4 + 5 > 3 §3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giácCBAViệtNamViệt hay Nam đi ngắn hơn??Việt đi ngắn hơn Nam vì BC BC AB + BC > AC BC + AC > AB 2. Hệ quả của bất đẳng thức tam giác* Hệ quả: Trong một tam giác, hiệu độ dài hai cạnh bất kì bao giờ cũng nhỏ hơn độ dài cạnh còn lại. Trong một tam giác, hiệu độ dài hai cạnh bất kì bao giờ cũng nhỏ hơn .độ dài cạnh còn lại. §3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giácBài tập 2. Điền vào chỗ trống: AB + AC > BC AB + BC > AC BC + AC > AB Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn và nhỏ hơn ... các độ dài của hai cạnh còn lại.hiệutổng§3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giácHãy thử vẽ tam giác với các cạnh có độ dài 1cm, 2cm, 4cm. Em có vẽ được không? Nhận xét: Không vẽ được tam giác nào có độ dài ba cạnh như trên1 cm2 cm?4cm? Em hãy vận dụng kiến thức vừa học để giải thích. §3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giácLưu ý: Khi xét độ dài ba đoạn thẳng có thảo mãn bất đẳng thức tam giác hay không, ta chỉ cần: +)So sánh độ dài lớn nhất với tổng hai độ dài còn lại +)Hoặc so sánh độ dài nhỏ nhất với hiệu hai độ dài còn lại. §3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác GHI NHỚ1) Bất đẳng thức tam giácĐịnh lí:AB+AC > BCAB+BC > ACAC+BC > AB2) Hệ quả của bất đẳng thức tam giácAB > AC - BC; AC > AB - BCBC > AB - AC; AB > BC - ACAC > BC - AB; BC > AC - ABABC§3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giácBài 18 (SGK trang 63) Cho các bộ ba đoạn thẳng có độ dài như sau:a) 2cm; 3cm; 4cmb) 1cm; 2cm; 3,5cmc) 2,2cm; 2cm; 4,2cmHãy vẽ tam giác có độ dài ba cạnh lần lượt là một trong các bộ ba ở trên (nếu vẽ được). Trong trường hợp không vẽ được, hãy giải thích.Phương pháp: Cách 1: So sánh độ dài lớn nhất với tổng hai độ dài còn lạiCách 2: So sánh độ dài nhỏ nhất với hiệu hai độ dài còn lại. Bài 18 (SGK trang 63) Cho các bộ ba đoạn thẳng có độ dài như sau:a) 2cm; 3cm; 4cmb) 1cm; 2cm; 3,5cmc) 2,2cm; 2cm; 4,2cmHãy vẽ tam giác có độ dài ba cạnh lần lượt là một trong các bộ ba ở trên (nếu vẽ được). Trong trường hợp không vẽ được, hãy giải thích.Ba độ dài 2cm, 3cm, 4cmXét 4 4 2 (thỏa mãn BĐT tam giác) nên chúng là ba cạnh của tam giác.b) Vì 1cm + 2cm AB – AC hay CB > 90 – 30 CB > 60Nếu đặt tại C máy phát song truyền thanh có bán kình hoạt động bằng 60km thì thành phố B không nhận được tín hiệub)Mặt khác theo bất đẳng thức tam giác ta có: BC BC.b) Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại.a) ΔABC có cạnh BC lớn nhất nên chân đường vuông góc kẻ từ A phải nằm giữa B và CHay H nằm giữa B và C ⇒ HB + HC = BC Trong ΔAHC vuông tại H ta có: HC 0 nên ta có: AB < BC + AC; AC < BC + AB GIẢIHƯỚNG DẪN TỰ HỌCHọc thuộc bất đẳng thức tam giác và hệ quả của BĐT tam giácLàm bài 15,17, 19, 21 SGK trang 63, 64