Bài giảng Hình học Khối 7 - Bài 2:Quan hệ giữa đường vuông góc và đường xiên và hình chiếu - Luyện tập
1. Khái niệm đường vuông góc, đường xiên, hình chiếu của đường xiên :
Cho điểm A không thuộc đường thẳng d (h.8). Hãy dùng êke để vẽ và tìm hình chiếu của điểm A trên d. Vẽ một đường xiên từ A đến d, tìm hình chiếu của đường xiên này trên d.
H là h/c của điểm A
HB là h/c của đường xiên AB
Bạn đang xem tài liệu "Bài giảng Hình học Khối 7 - Bài 2:Quan hệ giữa đường vuông góc và đường xiên và hình chiếu - Luyện tập", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
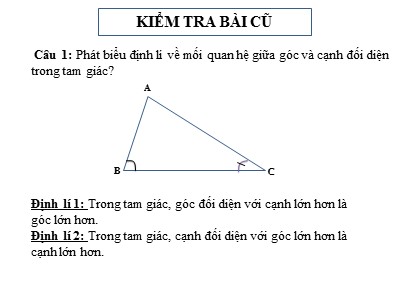
Câu 1: Phát biểu định lí về mối quan hệ giữa góc và cạnh đối diện trong tam giác?Định lí 1: Trong tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.Định lí 2: Trong tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.ABCKIỂM TRA BÀI CŨCâu 2: Trong một bể bơi, hai bạn Nam và Dũng cùng xuất phát từ điểm A, Nam bơi tới điểm B, Dũng bơi tới điểm C. Biết B và C cùng thuộc đường thẳng d, AB vuông góc với d, AC không vuông góc với d. Hỏi ai bơi xa hơn ? Hãy giải thích ?dBạn Dũng bơi xa hơn bạn Nam.Vì trong tam giác vuông ABC có là góc lớn nhất của tam giác, nên cạnh huyền AC đối diện với góc B là cạnh lớn nhất của tam giác.Vậy AC > AB nên bạn Dũng bơi xa hơn bạn Nam.KIỂM TRA BÀI CŨ- Ai bơi xa nhất ? - Ai bơi gần nhất ?ACHB§2. QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN, ĐƯỜNG XIÊN VÀ HÌNH CHIẾU. LUYỆN TẬPNỘI DUNG BÀI HỌCKhái niệm đường vuông góc, đường xiên, hình chiếu của đường xiênQuan hệ giữa đường vuông góc và đường xiênCác đường xiên và hình chiếu của chúngVận dụng1. Khái niệm đường vuông góc, đường xiên, hình chiếu của đường xiên Ad0 Cm12345678910THCS PhulacHBAH là đường vuông góc kẻ từ A đến d.H hình chiếu của A trên d (chân đường vuông góc) AB là một đường xiên kẻ từ A đến d.HB là hình chiếu của đường xiên AB trên d.§2. QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN, ĐƯỜNG XIÊN VÀ HÌNH CHIẾU. LUYỆN TẬP1. Khái niệm đường vuông góc, đường xiên, hình chiếu của đường xiên :Ad0 Cm12345678910THCS PhulacHB Cho điểm A không thuộc đường thẳng d (h.8). Hãy dùng êke để vẽ và tìm hình chiếu của điểm A trên d. Vẽ một đường xiên từ A đến d, tìm hình chiếu của đường xiên này trên d. §2. QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN, ĐƯỜNG XIÊN VÀ HÌNH CHIẾU. LUYỆN TẬPH là h/c của điểm AHB là h/c của đường xiên AB?12. Quan hệ giữa đường vuông góc và đường xiên : Từ một điểm A không nằm trên đường thẳng d, ta có thể kẻ được bao nhiêu đường vuông góc và bao nhiêu đường xiên đến đường thẳng d ? dA Định lí 1:Trong các đường xiên và đường vuông góc, đường vuông góc là đường ngắn nhất. ?2§2. QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN, ĐƯỜNG XIÊN VÀ HÌNH CHIẾU. LUYỆN TẬPĐịnh lí 1:2. Quan hệ giữa đườngvuông góc và đường xiên :Chứng minh :Độ dài đường vuông góc AH gọi là khoảng cách từ điểm A đến d.GTKLA dAH là đường vuông góc AB là đường xiênAH AC thì HB > HC a) Nếu HB > HC thì AB > AC Cho hình 10. Hãy sử dụng định lí Py-ta-go để suy ra rằng :Hình 10c) Nếu HB = HC thì AB = AC và ngược lại nếu AB = AC thì HB = HC ?4§2. QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN, ĐƯỜNG XIÊN VÀ HÌNH CHIẾU. LUYỆN TẬPBÀI 2. QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN, ĐƯỜNG XIÊN VÀ HÌNH CHIẾU.3. Các đường xiên và hình chiếu của chúng :a) Nếu HB > HC thì AB > ACHB > HC (gt)HB2 > HC2 AB2 > AC2AB > ACĐường xiên nào có hình chiếu lớn hơn thì lớn hơn.AH2 + HB2 > AH2 + HC2Áp dụng định lí pytago cho tam giác AHB vuông tại H và tam giác AHC vuông tại H :BÀI 2. QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN, ĐƯỜNG XIÊN VÀ HÌNH CHIẾU.3. Các đường xiên và hình chiếu của chúng :?4(SGK)b) Nếu AB > AC thì HB > HCĐường xiên nào lớn hơn thì có hình chiếu lớn hơn. AB > AC (gt)AB2 > AC2HB2 > HC2HB > HCAH2 + HB2 > AH2 + HC2Áp dụng định lí pytago cho tam giác AHB vuông tại H và tam giác AHC vuông tại :3. Các đường xiên và hình chiếu của chúng :c) Nếu HB = HC thì AB = AC và ngược lại nếu AB = AC thì HB = HC.Ta có : HB = HC (gt)Nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau. Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau.§2. QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN, ĐƯỜNG XIÊN VÀ HÌNH CHIẾU. LUYỆN TẬP3. Các đường xiên và hình chiếu của chúng :§2. QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN, ĐƯỜNG XIÊN VÀ HÌNH CHIẾU. LUYỆN TẬPĐường xiên nào có hình chiếu lớn hơn thì lớn hơn. Đường xiên nào lớn hơn thì có hình chiếu lớn hơn. Nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau. Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau.Định lí 2ÁP DỤNG Qua điểm A không thuộc đường thẳng d, kẻ đường vuông góc AH và các đường xiên AB, AC đến đường thẳng d (H, B, C đều thuộc d). Biết rằng HB AC (B) AB = AC(C) AC > AB (D) AH > AB GIẢITa có HB, HC lần lượt là hình chiếu của AB, ACtrên đường thẳng dVì HB HC;c) HB < HC.GIẢI:Vì AB < AC (gt) và AH ⊥ BC mà AB, AC là hai đường xiên có hình chiếu tương ứng là HB và HC nên HB < HCVậy đáp án c) đúng.cVận dụng: (bài 9 SGK trang 59)Để tập bơi nâng dần khoảng cách, hàng ngày bạn Nam xuất phát từ M, ngày thứ nhất bạn bơi đến A, ngày thứ hai bạn bơi đến B,ngày thứ 3 bơi đến C, Hỏi bạn Nam bơi như thế có đúng mục đích đề ra hay không (ngày hôm sau có bơi được xa hơn ngày hôm trước không)?Vì sao?Vận dụng: (bài 9 SGK trang 59)Các điểm A, B, C, D, cùng nằm trên một đường thẳng d+ Theo định nghĩa:MB, MC, MD, là các đường xiên kẻ từ M đến d.MA là đường vuông góc kẻ từ M đến dAB là hình chiếu của đường xiên MB trên dAC là hình chiếu của đường xiên MC trên dAD là hình chiếu cùa đường xiên MD trên d + Theo định lý 1, MA là đường ngắn nhất trong các đường MA, MB, MC, + Theo định lý 2: AB < AC < AD < nên MB < MC < MD < (đường xiên nào có hình chiếu lớn hơn thì lớn hơn)Vậy MA < MB < MC < MD < nên bạn Nam đã tập đúng mục đích đề ra. GIẢIdHướng dẫn về nhàHọc thuộc định lí 1, định lí 2 SGKLàm bài tập 10, 11, 12, 13 SGK trang 59, 60
Tài liệu đính kèm:
 bai_giang_hinh_hoc_khoi_7_bai_2quan_he_giua_duong_vuong_goc.ppt
bai_giang_hinh_hoc_khoi_7_bai_2quan_he_giua_duong_vuong_goc.ppt



