Bài giảng Toán Khối 7 - Bài 7: Định lý Pitago

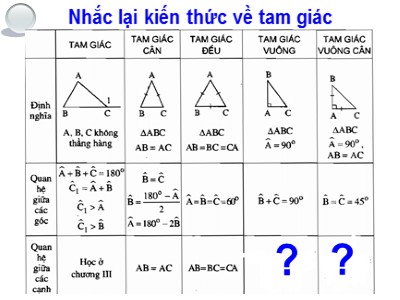
??Nhắc lại kiến thức về tam giácCó bao nhiêu cách chứng minh một tam giác là tam giác cân, tam giác đều, tam giác vuông? nêu cụ thể từng cách.Bài học hôm nay sẽ cho chúng ta biết thêm về quan hệ giữa các cạnh trong tam giác vuông và một cách nữa để chứng minh một tam giác là tam giác vuông. Nhắc lại kiến thức về tên các cạnh trong tam giác vuôngBACBC: cạnh huyềnAB và AC : hai cạnh góc vuông § 7: ĐỊNH LÍ PY-TA-GO 1. ĐÞnh lý Py-ta-goVÏ mét tam gi¸c vu«ng cã c¸c c¹nh gãc vu«ng b»ng 3cm vµ 4cm. đo ®é dµi c¹nh huyÒn.?13 45BACxy§ 7: ĐỊNH LÍ PY-TA-GO 1. ĐÞnh lý Py-ta-go?1/129 VÏ mét tam gi¸c vu«ng cã c¸c c¹nh gãc vu«ng b»ng 3cm vµ 4cm. đo ®é dµi c¹nh huyÒn.453 52 == 9 +16 =25 32 + 42 52 = 32 + 42 25?1/129 VÏ mét tam gi¸c vu«ng cã c¸c c¹nh gãc vu«ng b»ng 3cm vµ 4cm. đo ®é dµi c¹nh huyÒn.?2. Lấy giấy trắng cắt 8 tam giác vuông bằng nhau. Trong mỗi tam giác vuông đó, ta gọi độ dài các cạnh góc vuông là a và b; độ dài cạnh huyền là c. Cắt 2 tấm bìa hình vuông có cạnh bằng a + b.a) Đặt 4 tam giác vuông lên tấm bìa hình vuông như hình 121. Phần bìa không bị che lấp là hình vuông có cạnh bằng c, tính diện tích phần bìa đó theo c Hình 121Hình 122b) Đặt 4 tam giác vuông lên tấm bìa hình vuông như hình 122. Phần bìa không bị che lấp gồm hai hình vuông có cạnh là a và b, tính diện tích phần bìa đó theo a và bc) Từ đó rút nhận xét gì về quan hệ giữa c2 và a2 + b2abcabbaccbabaababcababcabccbccbbbcaaaaaaaaabbbbaccc2a2b2 Nhận xét: c2 = a2 + b2abcHình 121Hình 122a+ba+ba+ba+bc) Từ đó nhận xét gì về c2 và a2+b2a) Diện tích phần hình không bị che lấp tính theo c là c2b) Diện tích phần hình không bị che lấp tính theo a và b là a2 + b2 bb?2453 52 = 32 + 42 bca c2 = a2 + b2Nhận xét : Trong một tam giác vuông bình phương độ dài cạnh huyền bằng tổng các bình phương độ dài 2 cạnh góc vuông.?: Qua ?1 và ?2, nêu nhận xét về quan hệ giữa các cạnh trong một tam giác vuông? ABC; ¢ = 900BC2 = AB2 + AC2GTKLBACTrong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.*Định lý Py-ta-go:§ 7: ĐỊNH LÍ PY-TA-GO 1. ĐÞnh lý Py-ta-go?1?2HDVNPytago sinh trưởng trong một gia đình quí tộc ở đảo Xa-mốt, một đảo giàu có ở ven biển Ê-giê thuộc Địa Trung Hải. Ông sống trong khoảng năm 570 đến 500 trước Công nguyên. Từ nhỏ , Pytago nổi tiếng về trí thông minh khác thường. Ông đã đi nhiều nơi trên thế giới và trở thành uyên bác trong hầu hết các lĩnh vực quan trọng. Định lý Pytago đã được biết đến từ lâu trước thời của Pytago, nhưng ông được coi là người đầu tiên nêu ra chứng minh định lý này.Cách chứng minh của ông rất đơn giản, chỉ bằng cách sắp xếp lại hình vẽ.Chứng minh định lý Pytago: xem ?2/129Trong hai hình vuông lớn ở hình minh họa bên trên, mỗi hình vuông chứa bốn tam giác vuông bằng nhau, sự khác nhau giữa hai hình vuông này là các tam giác vuông được bố trí khác nhau. Do vậy, khoảng trắng bên trong mỗi hình vuông phải có diện tích bằng nhau. Dựa vào hình vẽ, hai vùng trắng có diện tích bằng nhau cho phép rút ra được kết luận của định lý Pytago.Nêu quan hệ giữa các cạnh trong tam giác vuông ?Cho ABC vuông tại B, hệ thức nào sau đây đúng?c/ AB2 = AC2 + BC2 b/ AC2 = AB2 + BC2 a/ BC2 = AB2 + AC2 sĐs?3. Tìm độ dài x trên hình 124, 125 AC2 = AB2 + BC2 ( định lí Py-ta-go)	 102 = AB2 + 82 100 = AB2 +64 AB2 = 100- 64 AB2 = 36 AB =EF2 = DE2 + DF2( định lí Py-ta-go) h.124h.125EF2 = 12 + 12 = 1+1= 2 Vậy x = EF = Xét tam giác ABC vuông tại B, ta có:Xét tam giác ABC vuông tại B, ta có:Vậy x = 6 = 6?4. Vẽ tam giác ABC có AB = 3cm, AC=4cm, BC=5cm. Hãy dùng thước đo góc để xác định số đo của góc BAC.C4A5B3Đo= 9009+16=2552 =32 + 42 = 52 = 32 + 42 25Nhận xét ABC có: 18 ABC; BC2 = AB2 + AC2¢= 900GTKLNếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.2. Định lí Py-ta-go đảo:BAC§ 7: ĐỊNH LÍ PY-TA-GO 1. Định lí Py-ta-go:Chứng minh định lý đảo Pytago: Gọi ABC là tam giác với các cạnh a, b, và c, với .Dựng một tam giác thứ hai có các cạnh bằng a và b và góc vuông tạo bởi giữa chúng. Theo định lý Pytago thuận, cạnh huyền của tam giác vuông thứ hai này sẽ bằng c = √ , và bằng với cạnh còn lại của tam giác thứ nhất. Bởi vì cả hai tam giác có ba cạnh tương ứng cùng bằng chiều dài a, b và c, do vậy hai tam giác này phải bằng nhau. Do đó góc giữa các cạnh a và b ở tam giác đầu tiên phải là góc vuông.Chứng minh định lý đảo ở trên sử dụng chính định lý Pytago. c2 = a2 + b2a2 + b2Hướng dẫn chứng minh định lý đảo Pytago: Có bao nhiêu cách chứng minh một tam giác là tam giác vuông? nêu cụ thể từng cách.Bài tập : Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:a) 6cm, 10cm, 8cm;b) 7cm, 7cm, 12cm; a) Ta có 102 = 62 + 82 =Vậy tam giác có độ dài ba cạnh 6cm, 10cm, 8cm là tam giác vuông (theo định lí Pytago đảo)Giải100; 36+ 64102 = 6 2 + 82 = 100 b) Ta có 122 =72 + 72 =49 + 49144; = 98 Vì 144 98 nên 122 72 + 72 suy ra tam giác có độ dài ba cạnh 7cm, 7cm, 12cm không là tam giác vuông (theo định lí Pytago đảo)53/sgk. Tìm độ dài x trên hình 127 x2 = 122 + 52 	 x2 = 144 + 25 x2 = 169 x = 292 = x2 + 212 x2 = 292 - 212 x =Áp dụng định lí Py-ta-go vàotam giác vuông, ta có:Áp dụng định lí Py-ta-go vàotam giác vuông ta có:= 13= 2054HDVNx2 = 841- 441= 400Hình aHình cTS5554. Đoạn lên dốc từ C đến A dài 8,5m, độ dài CB bằng 7,5m (h.128). Tính chiều cao AB	Giải Xét tam giác ABC vuông tại B, ta có:AC2 = BC2 + AB2( định lí Py-ta-go)8,52 = 7,52 + AB2AB2 = 8,52 – 7,52 AB2 = 72,5 – 56,25 = 16 AB == 4 (cm)HDVNTSTAM GIÁC AI CẬPTam giác có độ dài ba cạnh bằng 3; 4; 5 đơn vị được gọi là tam giác Ai Cập.Khoảng 1000 năm trước công nguyên, người Ai Cập đã biết căng dây có thắt nút thành 12 đoạn bằng nhau, gồm các đoạn có độ dài 3; 4; 5 để tạo ra một góc vuông.BT 55/SGK. Tính chiều cao của bức tường (H.129) biết chiều dài của thang là 4m và chân thang cách tường là 1m	 Áp dụng định lí Py-ta-go vàotam giác vuông ABC, ta có: AC2 = BC2 + AB2 42 = 12 + AB2 AB2 = 42 – 12 AB2 = 15 AB =Vậy chiều cao bức tường là (m)CAB1m4mChiều cao của bức tường là cạnh của tam giác vuông HDVNTS