Bài tập Đại số 7 - Chuyên đề: Tỉ lệ thức

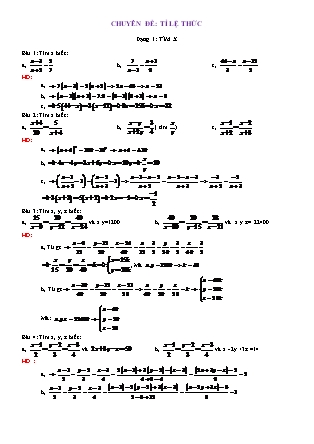
CHUYÊN ĐỀ: TỈ LỆ THỨC
Dạng 1: TÌM X
Bài 1: Tìm x biết:
a, 	b, 	c, 
HD:
	a, 
b, 	
c, 
Bài 2: Tìm x biết:
a, 	b, ( tìm )	c, 
HD:
a, 
b, 
	c, 
Bài 3: Tìm x, y, z biết:
a, và x.y=1200	b, và x.y.z = 22400
HD:
	a, Từ gt 
, Mà 
b, Từ gt
	Mà: 
Bài 4: Tìm x, y, z biết: 
a, và 	b, và x - 2y +3z =14 	
HD :
a, 
b, 
Bài 5: Tìm x, y, z biết:
a, và 	b, và 	
HD :
	a, Từ : =
b, Từ : =>
Bài 6: Tìm ba số x, y, z biết : và 
Bài 7: Tìm các số x,y,z biết chúng thỏa mãn đồng thời các điều kiện sau : và 
HD :
	Từ : 
	, Tương tự cho y và z 
Bài 8: Tìm x, y, z biết: 
a, và 	b, x:y:z=3:4:5 và 
HD:
	a, 
b, 
Bài 9: Tìm x, y, z biết:
a, và 	b, và 	
HD:
	a, 
b, 
Bài 10: Tìm các số x, y, z biết: 
a, và 	b, và 
HD :
	a, Từ GT ta có :
	b, 
Bài 11: Tìm x, y biết: và 
HD :
	Ta có : 
Bài 12: Tìm x, y, z biết: và 
HD :
	Từ GT ta có : ( Vô lý)
	Vậy không tồn tại x, y, z thỏa mãn :
Bài 13: Tìm x, y, z biết:
a, và x+y+z=49	b, và 	
HD:
	a, 
	b, 	
Bài 14: Tìm x, y, z biết:
a, và 	b, và 
HD :
	a, Từ : 
	Nên 
	b, Từ : => 
Bài 15: Tìm x,y,z biết: 
HD :
	Từ : 
	=>
	=> 
Bài 16: Tìm x, y, z biết : 
HD :
	Từ giả thiết => Cộng tử với tử ta được : 
	Khi đó : 
	Và 
Bài 17: Tìm x, y, z biết: 
HD :
	Từ GT => Tử + Tử + Tử =
	Khi đó : 
	Tượng tự để tìm ra y, z
Bài 18: Tìm x, y, z biết: 
HD :
	Từ GT=> Tử + Tử + Tử =>
	Khi đó : . Làm tương tự cho y và z
Bài 19: Tìm x, y, z biết: 
HD :
	Ta có : 
	Khi đó : . Tương tự cho y và z
Bài 20: Tìm x, y biết: 
HD :
	Từ 
Bài 21: Tìm x, y biết: 
HD :
	Từ , Thay vào tìm được y
Bài 22: Tìm x, biết: 
HD :
Ta có : , Thay vào tìm được y
Bài 23: Tìm x biết 
HD: 
=>
Nếu 5x-7y-7 # 0 thì , Thay vào ta được y=3. Nếu 5x-7y-7=0=> 5x-1=0=>
Bài 24: Tìm x, y biết: 
HD :
	Ta có : 
	. Thay vào tìm được y
Bài 25: Tìm x,y,z biết : 
Bài 26: Tìm x, y, z biết : 
Bài 27: Cho và . Tính b, c
HD :
	Từ : 
Bài 28: Cho và . Tính b, c
HD:
	Ta có: 
Bài 29: Tìm a, b biết: 
HD:
	Ta có: 
Bài 30: Tìm ba số thức x, y, z khác 0 biết : và 
Bài 31: Cho 3 số hữu tỉ bằng nhau: và , Tính giá trị của mỗi tỉ số đó
HD :	
Bài 32: Tìm x biết : , và các tỉ số đều có nghĩa
HD : 
Nếu a+b+c=0 thì b+c= -a, a+c= -b, a+b= -c khi đó 
Nếu a+b+c0 thì 
Bài 33: Tìm x, biết: ,
HD :
	Ta có : 
Bài 34: Tìm x, y, z biết: 
Bài 35: Tìm a, b, c biết: 
HD:
	Từ , và 
Bài 36: Tìm a, b, c biết: (a+b) : ( 8 – c): (b+c) : (10 +c)=2:5:3:4
HD :
	Từ 
	mà 
Bài 37: Tìm các số a, b, c Z biết : 
HD :
	Ta có : 
	, Vì 
	Do a,b,c nguyên nên 
Bài 38: Tìm x, y biết: 
HD:
	=>
	TH1: 
	TH2: 
Bài 39: Tìm ba số a,b,c biết: và a+b+c=-50
HD :
	Ta có : 
	=>
Bài 40: Tìm x,y,z biết : và 2x+3y-z=40
HD:
	Ta có: 
	=> 
Bài 41: Tìm x, y, z biết: và x+ y+ z=48
HD:
	Ta có: 
	=> 
	làm tương tự ta được: 
Bài 42: Tìm x, y, z biết: và 
Bài 43: Tìm x, y,z biết: và x+y+2z= -31
HD :
	Ta có : , Đặt (1) 
	 Đồng nhất ta được :
	 , Giả sử cho h=1 thì , Như vậy để cho chẵn thì ta nen cho h =7
	Khi đó : 
	Ta biến đổi (1) như sau :
	 , Cộng theo vế ta được : 
	Mà 
Bài 44: Tìm các cặp số a, b thỏa mãn: 
HD:
	ĐKXĐ: 
	Suy ra: 
	 , Với 
Bài 45: Tìm x,y,z biết : ; ; 
HD:
	Ta có: và 
	TH1: 1
	TH2: làm tương tự
Bài 46: Tìm các số: , biết: và 
HD: 
Áp dụng dãy tỉ số bằng nhau ta có: 
Bài 47: Tìm , biết rằng : , và 
Bài 48: Tìm số tự nhiên M nhỏ nhất có 4 chữ số thỏa mãn điều kiện: biết: a, b, c, d, e, f thuộc và 
HD: 
Từ gt=> => 
Tương tự ta có: và khi đó , và M là số tự nhiên nhỏ nhất có 4 chữ số nên M=1080
Bài 49: Tìm x,y biết: và x+y=22
HD :
	Ta có : 
Bài 50: Tìm x, y biết: và 
HD:
	Ta có: 
	Khi đó: và 
Bài 51: Tìm số hữu tỉ a,b biết : a-b=a :b và a-b=3(a+b)
HD:
	Ta có: 
	Mà thay vào 
	=..
Bài 52: Hãy tìm tất cả các số có hai chữ số biết rằng tổng, hiệu, tích của các chữ số của số đó là ba số nguyên dương và tỉ lệ với 35: 210: 12
HD:
	Gọi số cần tìm là: , Giả sử : a>b
	Theo bài ra ta có : 
	, Vô lý vì a, b cùng dấu.
Bài 53: Tìm hai số hữu tỉ a,b biết hiệu a và b bằng thương của a và b và bằng 2 lần tổng của a và b,
HD:
Theo bài ra ta có: 
Bài 54: Tìm x,y,z biết: 
HD :
Từ x+y=2z ta có : x-2y+z=0 hay 2x-4y+2z=0 hay 2x-y-3y+2z=0 hay 2x-y=3y-2z
Mà nên 2x-y=3y-2z=0. Từ 2x-y=0=>
Từ 3y-2z=0 và x+z=2y=> x+z+y-2z=0 hay hay hay 
=> . Vậy các giá trị x,y,z cần tìm là 
Bài 55: Tìm 3 phân số có tổng của chúng bằng , các tử của chúng tỉ lệ với 3:4:5 và các mẫu số tương ứng của chúng tỉ lệ với 5:1:2
HD :
Gọi 3 phân số cần tìm là thì ta có: và 
=> đó là ba phân số cần tìm
Bài 56: Số M được chia làm 3 số tỉ lệ với , tìm số M biết rẳng tổng bình phương của ba số đó bằng 4660
HD :
Ta có : 0,5 : : nên ta có : 
Giả sử M được chia thành 3 số là x ;y ;z.
Theo bài ra ta có :
=>
Vậy M=12+40+54=106 hoặc M=-106
Dạng 2: TÍNH GIÁ TRỊ CỦA BIỂU THỨC
Bài 1: Cho dãy tỉ số bằng nhau: 
Tính giá trị biểu thức: 
HD:
Từ GT trừ đi 1 vào mỗi vế của tỉ số ta có: 
	TH1: Nếu 
	TH2: Nếu 
Bài 2: Cho 3 số x, y, z khác 0 thỏa mãn: .Tính 
HD:
	Từ GT cộng thêm 2 vào mỗi vế của của tỉ số ta được:
	TH1: 
	TH2: 
Bài 2: Cho , 
Tính giá trị của biểu thức: 
HD:
	Ta có: 
	Vì 
Bài 3: Cho và dãy tỉ số: .
Tính: 
HD:
	Vì 
	 	 và , Thay vào 
Bài 4: Cho dãy tỉ số : 
Tính giá trị biểu thức: 
HD:
	Trừ 2011 vào mỗi vế của tỉ số trong tỉ lệ thức ta được:
	TH1: 
	Th2: 
Bài 5: Cho a, b, c thỏa mãn: 
Tính giá trị của biểu thức: 
HD :
	Từ GT ta cộng thêm 2 vào mỗi tỉ số trong dãy tỉ số bằng nhau có: 
	TH1 : 
TH2 : 
Bài 6: Cho a +b +c +d 0, và 
Tính giá trị biểu thức: 
HD :
	Từ GT nghịch đảo ta có => 
	Cộng 1 vào các tỉ số ta được : 
	 vì 
	nên 
Bài 7: Cho a, b, c thỏa mãn : , 
Tính 
Bài 8: Cho và , Tính 
HD:
	Từ GT ta có : 
TH1 :
	TH2 : => P=27
Bài 9: Cho a,b,c dôi 1 khác nhau và .Tính 
Bài 10: Cho a, b, c khác nhau và khác 0, t/m: . 
Tính giá trị của biểu thức: 
HD:
	Từ GT ta nghịch đảo => 
	Cộng 1 vào các tỉ số ta được : 
	TH1 : 
	TH2 : 
Bài 11: Cho 3 số x,y,z,t thỏa mãn: 
Và x+ y+ z+ t = 2012. Tính giá trị P= x+2y – 3z +t
HD:
Từ GT ta có: Cộng (n+1) vào mỗi tỉ số trong dãy tỉ số bằng nhau ta được:
	Thay vào ta tính được 
Bài 12: Cho , Tính giá trị của biểu thức: 
HD :
	Ta có : 
Bài 13: Cho 
Tính 
HD :
	Từ GT ta có : => 
Thay vào A ta được A = 2
Bài 14: Cho a,b,c là các số hữu tỉ khác 0, sao cho: 
Tính 
HD :
	Cộng thêm 2 vào GT ta được : 
	TH1 : 
	TH2 : 
Bài 15: Cho ,Tính 
HD :
	Từ GT nghịch đảo ta được :
	Cộng thêm 1 vào các tỉ số ta được : 
	TH1 : 
	TH2 : 
Bài 16: Tính A biết A= 
HD:
	Ta có : 
Bài 17: Cho và .Tính: 
HD:
	Từ GT ta lấy Tử + Tử + Tử + Tử ta được :
	Thay vào A ta được : 
Bài 18: Cho a,b,c khác 0, thỏa mãn : , Tính 
HD:
	Với a, b, c khác 0 , nghịch đảo giả thiết ta được :
	khi đó : 
Bài 19: Cho x,y,z là 3 số dương phân biết, Tìm tỉ số , biết:
HD:
	Từ GT ta có : 
Bài 20: Cho , Tính 
Bài 21: Cho , Tính giá trị của biểu thức: 
HD :
	Từ GT ta có :
Bài 22: Cho a-b=13, Tính giá trị của biểu thức: 
HD :
	Từ GT ta có : thay vào B ta được :
Bài 23: Cho 3 số a,b,c có tổng khác 0 và thỏa mãn: , 
Tính giá trị của biểu thức: ( Giả thiết các tỉ số đều có nghĩa)
Bài 24: Cho x: y: z = 5: 4: 3, Tính 
HD :
	Từ GT ta có : 
	Khi đó : 
Bài 25: Cho , Tính 
HD : 
Từ GT => (1)
(1)=> Và ( 1)=> 
Nên =1=> 
Bài 26: Cho , Tính P biết x,y,z tỉ lệ với 5 :4 :3
HD: 
Từ GT : thay vào ta được : 
Bài 27: Cho Hãy tính: 
HD:
	Từ GT ta có : 
Bài 28: Cho , Tính 
HD :
	Từ GT ta có : 
Bài 29: Cho Tính 
HD :
	Từ GT ta có : =>
Bài 30: Cho x:y:z=5:4:3 và 2x-3y+5z khác ) Tính giá trị 
HD :
	Từ GT ta có : 
Bài 31: Tính giá trị của các biểu thức sau: biết: 
HD :
	Từ GT 
Bài 32: Cho Tính 
HD:
	Từ 
Bài 33: Tính , biết a,b, c có quan hệ: 
HD:
	Từ GT ta có: 
Bài 34: Cho Tính 
Bài 35: Tính biết: 
HD :
	Vì 
Bài 36: Cho và .Tính A= x+y+z
HD :
	Từ GT=> 
	Thay vào A ta được : A
Bài 37: Tính biết: 
HD :
	Từ GT => Thay vào A ta được : 
Bài 38: Cho x = by +cz, y = ax +cz, z = ax +by và x +y +z 0. Tính giá trị : 
HD :
	Cộng theo vế của GT ta được : , Thay x, y , z trở lại ta có :
	Tương tự ta có : , Khi đó ta có : 
Bài 39: Cho a+b+c=2015 và , Tính 
HD :
	Ta có : 
Bài 40: Cho 3 số a, b, c thỏa mãn: 
Tính giá trị của biểu thức: 
HD:
Từ GT ta có: => 
Bài 41: Cho ba số a,b,c thỏa mãn: , Tính giá trị của biểu thức:
HD :
Từ GT ta có: 
Bài 42: Tính giá trị của: , biết: 
HD :
Từ GT ta có : 
Bài 43: Tính biểu thức: Với 
HD :
	Từ GT ta có :
Bài 44: Cho a, b,c khác 0 và đôi 1 khác nhau thỏa mãn : , 
Tính 
Dạng 3: CHỨNG MINH RẰNG
Bài 1: Cho . Chứng minh rằng:
a, 	b, 	c, 
HD:
	a, 
	b, 
	c, 
Bài 2: Cho . Chứng minh rằng:
a, 	b, 	c, Với a2=b.c thì 
HD:
	a, 
	b, 
	c, 	
Bài 3: Cho . Chứng minh rằng:
a, 	b, với thì 	c, 	
HD:
	a, 
	b, 
c, 
Bài 4: Cho , Chứng minh rằng:
a, 	b, 	c, 
Bài 5: Cho . Chứng minh rằng: 
HD:
	Ta có: 
Bài 6: Cho , Chứng minh rằng: 
HD:
	Ta có: 
Bài 7: Cho . Chứng minh rằng: 
HD:
	Từ: 
Bài 8: Chứng minh rằng : nếu Thì 
HD :
	Từ GT 
Bài 9: Cho , Các số x, y, z, t thỏa mãn : . CMR : 
HD :
	Từ GT ĐPCM
Bài 10: Cho tỉ lệ thức: , Chứng minh rằng: và 
HD:
	Từ 
	và 
Bài 11: Cho a, b, c R, và a, b, c 0, thỏa mãn: . Chứng minh rằng: 
HD:
Bài 12: Cho: , Chứng minh rằng: 
HD:
	Ta có: 
Bài 13: Cho , CMR: 
Bài 14: Cho 4 số thỏa mãn: , , Chứng minh :
HD:
	Từ GT => 
Bài 15: Cho 
HD :
	Từ GT ta có :
Bài 16: Cho a,b,c 0, t/m khi đó , Khi đó n = ? 
HD:
	Từ: 
	Mà 
Bài 17: Cho , CMR: 
HD : 
Ta có : 
Áp dụng tính chất dãy tỉ số bằng nhau : 
Bài 18: Cho , CMR : 
HD :
 	Đặt 
và 
Bài 19: Cho tỉ lệ thức: ,CMR: ,Với điều kiện mẫu thức xác định
HD:
	Đặt , Thay vào biểu thức ta có:
 và 
Bài 20: Cho các số a, b, c, x, y, z t/m , Chứng minh rằng: 
HD:
	Đặt: 
	 và và => đpcm
Bài 21: Cho , CMR : 
HD : 
=> 
Bài 22: CMR : nếu thì 
HD:
	Ta có: 
Bài 23: Cho 
HD :
	Ta có : 
 Bài 24: Cho , Chứng minh rằng:
a, 	b, 
HD:
	a, Từ GT ta có: 
Bài 25: Cho a,b,c,d là các số hữu tỉ dương và , CMR : 
HD :
	Từ GT và 	(2)
	Từ (1) và (2) Nhân chéo
Bài 26: Cho , cmr: 
HD: 
Từ gt=> , Khi đó: 
=> hay 
Bài 27: Cho , CMR: 
HD: 
Từ gt=> 
=> 
Bài 28: Cho 
HD :
	Từ GT 
Bài 29: Cho 
a, 	b, 
HD :
	a, Vì 
	b, 
Bài 30: Cho và 
HD :
	Từ GT 
Bài 31: Cho , Chứng minh rằng: 
HD:
	Ta có: 
Bài 32: CMR: Nếu thì 
HD :
	Ta có : 
Bài 33: Cho 
HD :
	Từ GT Nhân chéo=> ĐPCM
Bài 34: Cho 
HD :
	GT=> 
Bài 35: Cho 
Bài 36: CMR : Nếu thì 
Bài 37: Cho và , CMR: 
HD:
	Từ GT => => 
Bài 38: Cho , Với a, b, c, d 0, Chứng minh rằng: hoặc 
HD:
	Ta có: 
TH1: 
	TH2: 
Bài 39: Cho 
HD:
	Từ GT, Ta nhân chéo rồi rút gọn:
	Hoặc : , Trừ 1 vào 2 vế ta được : 
Bài 40: Cho và , CMR: 
Bài 41: Cho tỉ lệ thức:, Chứng minh rằng: c = 0
HD:
	Ta có: 
Bài 42: Cho tỉ lệ thức : , CMR : a=0
HD: 
Từ => 
Nếu ta có vô lý=> a=0
Bài 43: Cho a, b, c, d t/m : , và a+b+c+d0, Chứng minh rằng: a= b= c= d
HD:
	Từ GT ta có: => 
Bài 44: Cho 
HD :
	Từ GT cộng từ với tử, mẫu với mẫu
Bài 45: Cho tỉ lệ thức: , CMR : 
HD:
Bài 46: CMR: nếu a+c=2b và 2bd=c(b+d) thì với b,d khác 0
HD: 
Vì a+c=2b nên từ 2bd=c(b+d) ta có: (a+c)d=c(b+d) hay a.d=b.c=> 
Bài 47: Chứng minh rằng: , Thì 
HD: 
Ta có: và 
và và 
Từ (1) và (2) ta có: 
Bài 48: Cho và CMR 4 số a, b, c, d có thể lập thành 1 tỉ lệ thức:
HD :
	Vì 
Bài 49: Cho , Chứng minh rằng 3 số a,b,c 0, thì có thể lập thành 1 tỉ lệ thức
HD :
	Vì : 
Bài 50: Chứng minh rằng : Nếu có a, b, c, d thỏa mãn : 
 thì chúng lập thành 1 tỉ lệ thức :
HD :
	Từ GT=> đpcm
	TH2 : ( Vô lý)
Bài 51: Cho , Chứng minh rằng, Giá trị của M không phụ thuộc vào x,y thì 4 số a,b,c,d lập thành 1 tỉ lệ thức :
HD :
	Đặt 	Chọn 
	Chọn 
Bài 52: Chứng minh rằng : Nếu và thì 
HD :
	Từ GT , Nhân vào=> ĐPCM
Bài 53: Cho x,y,z là các số khác 0 và CMR : x=y=z
HD : 
Từ gt=> 3 cặp phân số bằng nhau	
Bài 54: Cho a,b,c,d,e,g , Biết rằng b,d,g>0 và a.d - b.c=2009 và c.g - d.e =2009
a, So sánh 	b, So sánh:
HD :
	a, Từ GT ta có :và 
	b, Từ GT ta có : 
Bài 55: Chứng minh rằng : Nếu thì , Đảo lại có đúng không ?
HD :
	Từ GT 
	Ngược lại : , vẫn đúng
Bài 56: Cho , 
Chứng minh rằng: 
HD:
	Từ GT=> 
	=
	=> (đpcm)
Bài 57: Cho , Chứng minh : 
HD:
	Từ GT=>
	=
Bài 58: Cho , CMR: 
Bài 59: Cho , CMR: 
HD:
	Nghịch đảo GT ta được: 
Bài 60: Cho dãy tỉ số: , Chứng minh rằng: 
HD:
	Từ GT =>
	=>
Bài 61: Cho , CMR: 
HD:
	 => 
Bài 62: Cho dãy tỉ số bằng nhau: , Chứng minh rằng: 
HD :
Từ GT ta có :
=> và 
Bài 63: Cho dãy , Chứng minh rằng: 
HD:
	Ta có: 
	 và => VT= VP
Bài 64: Cho 3 số x,y,z thỏa mãn: , CMR : 
HD: 
Từ gt=> => 
Bài 65: Cho 3 số x,y,z thỏa mãn: by+cz=a, ax+cz=b, ax+by=c , với a,b,c là các số dương cho trước thì không phụ thuộc vào a,b,c
HD:
	Cộng theo vế các GT ta được: 
	Chứng minh tương tự ta có: 
	Khi đó: 
Bài 66: Cho , Chứng minh: 
HD:
	Đặt: 
	=> 
	Chứng minh tương tự: và => đpcm
Bài 67: Cho a, b dương thỏa mãn: , Chứng minh 
HD:
	Giả sử: a=1=>b=1=> . Nếu: , Giả sử: 
	=> , Vì 
Bài 68: Cho a,b,c0 và , chứng minh rằng: 
HD:
	Từ GT=> 
	=>, Tương tự: 
	Cộng theo vế ta được: =>
Bài 69: Cho , Chứng minh (1+x)(1+y)(1+z)=(1-x)(1-y)(1-z)
HD:
	Xét , Tương tự: 
	Khi đó 
	Tương tự: , 
	Khi đó: 
Bài 70: Cho và Chứng minh rằng: 
HD:
	 Từ 
Bài 71: Chứng minh rằng nếu: Thì 
HD:
	Xét , Tương tự: 
	Khi đó 
	Tương tự: , 
	Khi đó: 
Bài 72 : Biết và và và , CMR : 
HD:
	Ta có: 
Bài 73: Cho và Chứng minh rằng: 
HD:
	Từ (1)
	Và thay vào (1) ta được: 
Bài 73: Cho các số hữu tỉ: với a,b,c,d số nguyên và b,d>0. 
CMR: nếu x<y thì x<z<y
HD: 
Vì Xét tích => 
Cmtt ta có: 
Bài 74: Cho 3 số a, b,c đôi 1 khác nhau, CMR: 
HD :
	Ta có : 
	Tính tương tự ta có : , và 
	Cộng theo vế : 
Bài 75: Cho , CMR: 
HD:
	Từ GT ta có: 
	Và 
	Nên đpcm
Bài 76: Chứng minh rằng nếu: , và a, b, c khác nhau và khác 0, thì:
HD:
	Vì a, b, c 0, chia giả thiết cho
 => ĐPCM 
Bài 77: Cho 4 số nguyên dương a, b, c, d trong đó b là trung bình cộng của a và c và , Chứng minh rằng : 4 số đó hợp nên 1 tỉ lệ thức :
HD :
	Vì và , Chuyển về bài trên 66
Bài 78: Cho Nếu , thì P không phụ thuộc vào x
HD :
	Đặt rút ra rồi thay vào P
Bài 79: Cho 
Chứng minh rằng : Có giá trị nguyên
HD:
	Từ GT ta có: 
	=> 
	TH1: 
	TH2: 
Bài 80: Cho A, B, C tỉ lệ với a, b, c, CMR : không phụ thuộc vào x, y
HD :
	Ta có : 
Bài 81: Cho các số a,b,c,x,y,z thỏa mãn : và ( Các tỉ số đều có nghĩa), CMR : 
Bài 82: Cho a, b, c khác 0 thỏa mãn: , CMR: 
Bài 83: Cho a, b, c tỉ lệ nghịch với , ( Giả sử các số trên và b+c, c+a, a+b đều khác 0), Chứng mỉnh rằng tỉ lệ thuận với